ガウス_レジャンドルの積分式を眺める

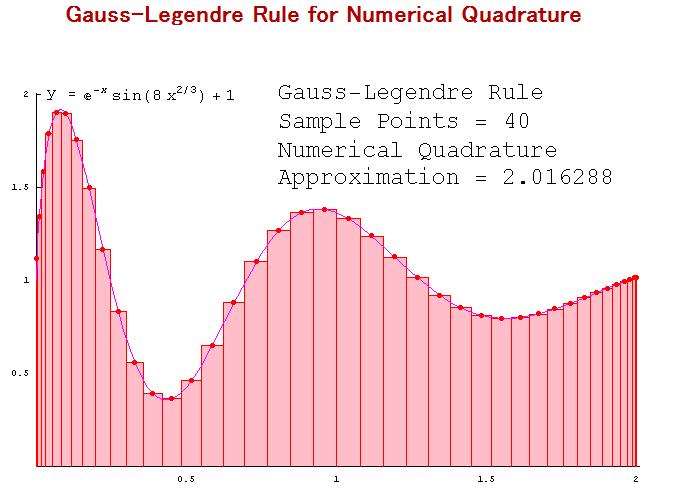
上図は積分点を増加させてゆくにつれて関数の求積の様子が変化していることを示すアニメの画像のスクリーンショット。URLは下記。
http://www.ecs.fullerton.edu/~mathews/a2001/Animations/Quadrature/GaussLegendre/GaussLegendreaa.html

本稿は自分用のメモを兼ねています。
１）画像の式以前にで積分点と重みの数値の精度が重要。
２）画像の式では割り算は２で割る計算のみ。あとは加算と乗算であり、この式からは誤差はほとんど発生しないと考えてよい。
３）楕円の１/４周長の計算を実施し、カシオの計算サイトの出力値と比較。楕円率99.9％の楕円においてようやく2048積分点数で誤差が大きく出現するが、1024点では余裕をもって16桁目四捨五入でも誤差ゼロ。
４）上記結果から推論すると1024点と2048点の中間あたりで積分点と重みの1５桁精度の利用結果が崩れると考えられる。原因は計算誤差(桁落ち）の蓄積。（with Excel2003)
５）４項の積分点と重みのデータに関しては当方のソフトを利用する限り、数万点でも誤差はほとんどでない。
６）積分点と重みのデータに関して精度を保つ理由は、(有）ゴットフット企画のURLにさりげなく記載されている。下図画像で２分法により解を求めたとあります。ニュートンラプソン法を利用してはこの場合は薦められないのです。