油圧システム＿ロジック弁

画像は下記ＵＲＬより引用しました。
http://www.yuken.co.jp/japanese/pdf/G495502.pdf
油圧回路設計でロジック弁を利用された経験のある方は、油圧回路設計のエキスパートと自称してもおかしくないと思います。超高圧（250～350ｋｇｆ/ｃｍ＾2）、超大流量（500ｌmin以上）になると普通のバルブでは極めて非効率になり、ロジックバルブの出番になります。２００ｋｇｆ/ｃｍ＾２、90l/minレベルでもコストさえＯＫならロジック弁の利用もあるかもしれません。ロジック弁を使う場合、パイロット回路にカートリッジタイプのバルブとの組合せが一般的と思います。
一般には圧力、流量が比較的少ない場合はカートリッジ型、一般には積層型、高圧大流量にはロジック弁と使い分けられています。私自身はロジック弁は使用した経験はないのですが、超大型パワーショベル、超大型ダンプ、プレス機械などに利用されていると思います。圧力損失が極めて少ない（発熱が少ない）特長から、普通の油圧装置にも使われだしているかもしれません。しかし、使いこなすにはバルブメーカーのアドバイスを受ける必要があります。またロジック弁を利用した配管系にはフランジ形の継手を使うほか、利用ホース、クランプ方法・・・その他関連する配管設計の知識も必要になります。

Pro/E(WF2,WF3)の操作マニュアル（Ｗｅｂ）

画像は下記ＵＲＬより引用しました。私、Ｐｒｏ／Ｅの２００１からＷＦ２のバージョンＵＰ時に操作方法が判らずここのＵＲＬを眺めながら操作を習得していったものです。ノートパソコン（現在修理待ち）にデータが入っているためにＵＲＬの名前が判らなかったのですが、偶然のきっかけで本日見つけました。
引用元：http://www005.upp.so-net.ne.jp/kirin/ProE_WF/ProE_W_Index.html
このＵＲＬはリンクにも登録しておきます。画像はまがり歯かさ歯車のピニオンのモデル例。このモデリング方法が記載されています。実用性はともかく取説の作成などには最適の手法かもしれません。このＵＲＬを眺めたときに凄いテクを持っている人材がいると新鮮な印象を抱いたものでした。はすば歯車にも応用がきくと思いますが、実用的には私は可変断面スィープの利用には疑問を持つので別の手法を採用しています。しかし、取説などにはこの手法でも十分でしょう。
追記：紹介のURLは抹消された様子です。英文ですが下記URLなど参考URLがまだWebに存在するので、ご参考に。
http://www.sharptechdesign.com/
ここには、通常モデル、サーフェス、メカニズムなど参考データを添えて紹介してあります。（09.05.19）

インボリュートスプラインの応力計算＿２

画像は下記ＵＲＬより引用しました。
http://www.rs.noda.tus.ac.jp/nog/sekkei1/s1-7.pdf
東京理科大学の野口研究室のＵＲＬで講義資料の一部です。ここの講義資料は問題に対する解答を示していないために部外者の私には答えのない問題演習を強いられます。それでも有益な資料類です。画像の公式はインボリュートスプラインの応力と伝達トルクの関係式です。
伝達トルク＝効率（0.75が普通）＊スプライン有効径（ピッチ円径）＊歯数＊歯の接触高さ（２＊ｍ－歯先の丸み半径）＊スプラインの接触長さ（スプライン穴の長さ）*許容面圧（材料による）/２
ということになります。先にＵＳＡのＺＡＫＵＧＥＡＲ社の式の紹介をしましたが、ＺＡＫＵＧＥＡＲ社の場合はＡＮＳＩ規格のスプラインを対象としているものと思われるので、日本の場合はこちらの公式がよいと思われます。ただ、この式の効率を０．７５としたのは一般的な場合で正確にはいろいろな条件を加味した数値を設定する必要があるかもしれません。この場合、ＺＡＫＵＧＥＡＲ社の式が参考になると思います。

Pro/MECHANICA について

現在、ライセンスは持っていないのだが、メカニカを使う環境が近所（といっても車が必要）にあるので、利用に困ることはない（定常的に使う訳ではない）。ここで客先からの解析依頼を処理する。Ｐｒｏ／ＭＥＣＨＡＮＩＣＡの長所はメッシュ切りに苦労しないことだろう。昔のＡＮＳＹＳ環境での苦労が嘘のようです。画像のようにＰｒｏ／ＥＮＧＩＮＥＥＲで細部までモデリングしたデータをそのまま利用できることも大きな長所です。これにはアダプチブＰ法という解析手法が大きくものをいっている。更に、解析結果の検証手段（信頼性評価手段）があることも関連している。先に紹介した曲がり梁の応力などはＭＥＣＨＡＮＩＣＡの利用で信頼性のある結果が得られる。もっと評価、重宝してよいと思います。画像は下記ＵＲＬより引用させて頂きました。
http://www.e-sentan.com/mec_character.html

WF2(Pro/E)の操作テキスト（和文）

画像の出典は下記より。Ｐｒｏ／Ｅの操作テキスト（和文）が少ないのは以前、記しましたが、テキストを眺めながら読み進めてゆける資料です（ＰＤＦ）。
zgkw3.sd.kanagawa-it.ac.jp/proe/getting_started_WF2.pdf
私自身がある程度マスターしていることもあるけれど、定常的に操作している訳ではないので、その立場からの操作テキストと見ても良いと思います。一応操作をマスターされている方もダウンロードされて眺められることを勧めます。

シェアウエアのダウンロードを可能にしました

シェアウエアのダウンロードを可能にしました。プロフィールをクリックするとシェアウエアのブログの所在が判ります。試行版は制限がありますが、評価には十分と思います。Ｖｅｃｔｏｒ社からもダウンロードは可能ですが、更新が遅れます。

オーストリア中央銀行ファボリーテン支店

オーストリアのウィーン市１0区のファボリーテン通りにある怪獣の面構えの建物。画像は下記ＵＲＬより。
http://homepage3.nifty.com/archi-jpg/a_map/austria/favoriten.html　説明もここが詳しい。驚かされるのはこの建物に同じ部品は一つも使われていないという事実です。オーストリアの現代建築の一つの極みといえるかもしれません。この建物の内部はれっきとした銀行ですが、その入り口がバーショップ・・・日本流にいえば飲み屋さんです。恰幅のいいママさん売り子さんが切り盛りしていたが、私が行ったのは閉店後の夕暮れ時でした。平日の昼間も営業しているのだろうか？？？

疲労限度線図の作り方と利用法

追記 2017.03.29
Googleの仕様の変更なのか不明ですが、下記画像のリンクが効かないようです。
関連画像を下記PDFにまとめました。必要な方は下記リンクよりダウンロードしてください。


http://m-sudo.sakura.ne.jp/soft_data/kikaikougaku(PDF)/HirouGend_Senzu.pdf

下記画像はすべて含まれています。

-------------------------------------------------------------------------------

追記 2015.12.22  元データが見つからないために下記の検証が不能な状態です。
下記URLを参照してください。
http://m-sudo.blogspot.jp/2009/05/blog-post_4655.html

画像の引用は下記より。
www.me.tokushima-u.ac.jp/zairyoukyoudo/17/t5-2.pdf
この疲労限度線図は自分でグラフを作成して利用することが大切です。領域ＡＤＥＣ内であれば疲労に対して安全に利用可能な範囲を示しています。
下図は具体的な疲労限度線図のデータプロットの方法の図示。

追記：疲労限度の数値が平滑、傷の無い標準試験片のデータである場合、おおむねその40％の数値が安全率を考慮した許容応力として採用されると考えてください。（疲労限度の数値に幅があるときは最も少ない数値を利用するようにします　変更：50％＝＞40％　2009.04.15　記）
http://m-sudo.blogspot.com/2009/04/blog-post_3367.html参照
2008.04.02
http://m-sudo.blogspot.com/2009/05/blog-post_4655.html参照
2009.05.14

最新の疲労限度に関する研究

画像は下記ＵＲＬより引用しました。
http://www.nachi-fujikoshi.co.jp/tec/pdf/
この論文によると私が従来解釈していた疲労限度の存在が特定の材料において否定されていることになります。現在の私の経験レベルではこの論文内容は記述してあることの概要を私なりに解釈するしか能がないので、志のある設計者諸兄には是非ともこの内容を他の文献をも参照しながら理解して欲しい。ＳＮＣＭ439という比較的一般性のある合金鋼の焼戻し処理は一般に６００度Ｃで水冷３３０ＨＢ程度の硬度を得る処理を行う必要があるのですが、より低温領域の焼戻し処理で高硬度を維持しようとすると論文の説明のように疲労限界がなくなるというものです。直感ですが合金鋼一般にもいえる可能性があるので材質に応じた規定の熱処理を行う必要性があると思います。ＳＭ443（マンガン鋼）、ＳＣＭ４３５～ＳＣＭ４４３（クロモリ鋼）などその対象かもしれません。従来軸受け鋼として利用されていたＳＵＪ２（高炭素クロム鋼）が完全に疲労限度が存在しないとなるとその衝撃は大きいですね。ＳＵＪ２はすべり軸受けの材料として使われていたそうですから。私個人的にはＳＮＣＭ材やＳＵＪ２、高速度鋼の使用経験がないのでよそ事といえばそういえるのですが・・・。この論文（ＰＤＦ）のＵＲＬをリンクに追加しました。

追記　本記事に関して技術士の方からコメントを頂きました。コメントに関連する疲労限度（寿命）の考察に
関して下記の記事があります。ご参考に。（2009.06.27記）

追記　上記データの出所のＵＲＬが異なっていました。下記に訂正します。（2010.07.28）
http://www.nachi-fujikoshi.co.jp/tec/pdf/14A1.pdf

曲がり梁の計算

追記）下記リンクを優先して読んでください。(2014.1018)

http://m-sudo.blogspot.jp/2014/03/blog-post_4.html
http://m-sudo.blogspot.jp/2013/03/blog-post_24.html

i以下データが旧いので参考程度に。

画像は下記ＵＲＬからの引用です。http://www.jniosh.go.jp/publication/RR/abst/RR-2001.htm
フック、Ｕボルト、リンクチェーンなどの強度計算に利用される曲がり梁の計算式への疑問を記載されています。ただでさえ、複雑な曲がり梁の式の利用には軽い頭痛を覚えますが、この警鐘はある意味で衝撃的でさえあります。理論による手計算の否定の結果として有限要素解析の利用が勧められています。Ｐｒｏ／ＭＥＣＨＡＮＩＣＡなどの有限解析ソフトの場合はモデルを単純化する必要もなく、実際の形状のままで解析が可能なことからこの命題に対して有効と思います。Ｐｒｏ／ＭＥＣＡＮＩＣＡのアダプチブ解析手法はメッシュ作成などは不要なために設計者にとっては実に利用しやすい。ただ、特異点などの発生の様子が見えた場合はモデルに対して何らかの近似的工夫を与える必要がありますが、その特異点の発生の有無の確認がＰｒｏ／ＭＥＣＨＡＮＩＣＡでは割合に容易であることからも、表題のような形状に対してはＰｒｏ／ＭＥＣＨＡＮＩＣＡの利用が現実的な解決手段と思います。尚、手計算での曲がり梁は緩やかな曲がりには適用は可能とは思いますが、計算ミスもしやすく、その場合でもＰｒｏ／ＭＥＣＨＡＮＩＣＡを利用するべきでしょう。某重工の冶工具としてのフックの強度計算には曲がり梁の式に補正を加味した計算式が採用されています。（補正はグラフからの読取り値）。詳細はノウハウのため紹介はできない。

追記）曲がり梁の公式は下記に掲載。
　　　http://m-sudo.blogspot.jp/2010/06/blog-post.html
　　　曲がり梁の形状係数
　　　http://m-sudo.blogspot.jp/2012/06/blog-post.html
（上記本文の文意はこの形状係数を加味することでＯＫかどうか、要確認）曲がり梁の最大応力を求めるための係数。貴重なデータです。（但し、ＪＩＳではなくピーターソンの理論より。ピーターソンの応力集中係数はＵＳＡでは標準的なデータです。円径断面、四角形断面しか掲載していないが、他の断面も推測してみることも大切と思います。）

油圧：分集流弁

画像は下記ＵＲＬより引用です。（高美精機株式会社）
http://www.kei.or.jp/takami/
油圧回路の流量を同調させるためのバルブ。特許を取得している部品だが、何故か似た構造のバルブが某油圧メーカーから販売されている。本元は高美精機株式会社と思います。リフターなどの複数のシリンダー同調への利用には注意が必要。センサーなどを利用したサーボバルブなどを利用するまでもない程度の同調システムへの利用には効果があると思います。シリンダーなどでの利用の場合は、ストロークエンドで誤差の吸収を行うことになります。ストローク途中の方向切換えは誤差が蓄積されるのでこの機能が必要な機構には利用は不可。
追記　参考ＵＲＬ
http://www.kei.or.jp/takami/
http://www.takami-seiki.com/explanatory2.pdf

Ｐｒｏ／Ｅの操作テキスト（国内版）

Ｐｒｏ／Ｅを利用されている皆さんには既にご承知のことと思いますが、東海大学ではＰｒｏ／Ｅの操作に関する説明書を、同大学での教習用に利用という条件で公開しています。メカニズムとサーフェスという魅力的な内容です。従って、教材というだけではなくＰｒｏ／Ｅの機能を紹介するテキストとしての存在感もあり、Ｐｒｏ／Ｅを利用しない方がたへのＰｒｏ／ＥのＰＲとしても、ここで紹介する価値があると考えました。ご承諾お願いします。Ｐｒｏ／Ｅに関しては上智大学も大変優れた操作説明書を刊行されており、他にも中央大学も書籍の刊行をされているそうです。特に上智大学の書籍にはトップダウンモデリングの手法が具体的にわかりやすく記載されており、個人的にはとても参考になったと思います。さて、東海大学のサーフェス操作の説明書にはスタイルサーフェスの要諦が記されていてとても参考になりました。私はスタイルサーフェスのライセンスを持っているのですが、この機能を利用したモデリングの依頼があれば有償になりますけれども、比較的格安に受託することも検討しています。
（但しＷＦ2.0，ＷＦ3.0のみ対応）
スタイルサーフェスの詳細な説明書はＵＳＡの有償のマニュアル（英文）が最適です。私は、こちらから習得しました。

右の画像はスタイルサーフェスを利用した例です。
出典は下記ＵＲＬより。
http://www.cc.u-tokai.ac.jp/text/2005/PROE_Surface.pdf

IEでの表示不良について

ある方からメールが送られてきて、画像の表示が変とのこと。ＩＥを利用しているとどうも表示が変らしい。ＩＥで利用してみると、画像がダブリ表示されていて見難い。ＦｉｒｅＦｏｘでは正常に表示されるのに、これは何だろうか？。当方はＵＲＬのコードはよく理解できないのですが、どなたか、原因が想定可能な方、メールでご教示頂けないでしょうか。困っているので、よろしくお願いいたします。

２０世紀初期の建築物（Ｗｉｅｎ）

閑話休題：画像及び文章の出典は下記
http://www.heuriger2005.com/tourismus/gebaude.html
ウィーンの中心部からドナウ河に沿って上流側に電車で２０分ほどのウィーンの森の入り口にある。建造時期にしては垢抜けた建物でした。ウィーンへ行ったら一度は訪ねたい。この建物の反対側は気分のいい芝庭だったが、物乞いに付きまとわれてしまった。ここから電車で二つ目の駅だったか、日本人学校のある町に出る。ウィーンに長期滞在するときに朝日新聞（日本語）などの売店があって重宝するが遅くなると売り切れてしまう。

無電解ニッケルメッキ

画像は下記ＵＲＬより引用しました。無電解ニッケルメッキはおよそほとんどの材料に利用可能ですが板金溶接構成品の面取り穴などメッキがうまく渡らない場合もあります。銀白色の光沢があり、表面は美観を呈しています。メッキ厚さなどの情報は下記ＵＲＬ参照ください。（画像引用元共）
http://www.kinzokuh.co.jp/ggijyutu2.html
メーカに発注する際は変色防止の後処理過程でのRoHS対応を確認してください。

リン酸塩処理

下記ＵＲＬより引用しました。油圧配管、マニホールド内部の防錆を目的として利用したりします。ここで留意したいことは浴槽のサイズが表記されていることです。このサイズからはみ出る部品は処理を引き受けてもらえない可能性があります。設計の際に留意する事項の一つです。
画像の引用元のＵＲＬ：http://www.parker.co.jp/jigyousyo_annai/katsuta.shtml

インボリュートスプラインの応力計算

画像はＵＳＡのＺａｋＧｅａｒ社のＵＲＬより引用。
http://www.zakgear.com/Calculators.html
ここのＵＲＬにはインボリュートスプラインの埋め込み式の応力オンライン計算シートがあります。利用している公式も記載してあるので必要な方にはご利用をお奨めします。スプラインの応力計算式自体は一般化されていないだけにとても有用なＵＲＬです。

玉軸受の損傷解析（Ｐｒｏ／Ｍｅｃｈａｎｉｃａ）

高知工科大学のライブラリから引用しました。画像は玉軸受に損傷が生じた場合の様子をＰｒｏ／ＥＮＧＩＮＥＥＲのＦＡＥ解析ソフト（Ｐｒｏ／Ｍｅｃｈａｎｉａ）で解析した接触圧力の検証の様子です。
論文のＵＲＬは
www.kochi-tech.ac.jp/library/　の中の
www.kochi-tech.ac.jp/library/ron/2002/2002mech/1030125।pdf（画像の出典も同じです。）
この論文はＰｒｏ／Ｍｅｃｈａｎｉｃａの利用方法としての教材の側面も持っています。Ｍｅｃｈａｎｉｃａを操作される機会のある方には一読を勧めたい内容です。私は現在Ｐｒｏ／Ｍｅｃｈａｎｉｃａを利用可能な環境にはないのですが過去に様々な解析を行った経験があるので機会がありましたら解析例を紹介しようと思います。尚、本論文の内容は（設計：玉軸受けの損傷解析）　としてリンクに記録します。

続：キー溝のある軸の強度

（株）小野測器のカタログ（ＰＤＦ）にも記載があるので紹介します。
http://www.onosokki.co.jp/HP-WK/whats_new/catalogs/pdftop.html
ここの中のデジタルトルクメータのカタログがあります。ここに軸の設計に関する主要項目が記載されています。軸の設計には多様な設計要素があり、自分でエクセルなどで計算フォームを作成することが肝要です。このカタログの所在にリンクを設定します。
設計：（株）小野測器のデジタルトルクメータカタログ（ＰＤＦ）

キー溝のある軸の強度

画像は下記ＵＲＬより引用。以前にも紹介しましたが、設計のベテランでも一通り目を通して置きたいＵＲＬです。キー溝の影響を受けた強度計算の公式を初めてみた。当方は従来はキー溝では怖いのでスプライン継ぎ手を利用していたがコスト上の問題点があります。しかし、キー溝の場合でも加工不良があるとどうにもならない。（キー溝の加工不良の実物検査ははめあい公差など面倒です。）高価でもインボリュートスプラインなら割合に安心感を抱いています。http://www.rmc.mce.uec.ac.jp/webclass.html

エクセルＶＢＡ小技集（リンク紹介）

エクセル散布図の機能利用による歯形形状の図形表示化に参考になったＵＲＬです。散布図のＸ目盛りとY目盛りを揃えることによって図形表示を設計データなど工業関係の利用に有効に利用できるようになりました。 他にも参考にさせて頂いた項目が豊富です。
http://hp.vector.co.jp/authors/VA033788/kowaza.html#0077
リンクに追加しました。

歯元の曲線のカーブと転位

図は転位歯形曲線です。M=5,Z=23で転位量が-2,0,+2 標準ラック工具で創成加工した形状です。（ラックの歯先Rは0.02）内側（中心寄り）は-転位、外側は+転位となります。中央で一部切れ込みの浅いカーブは　Z=17のピ二オンカッタで切削加工をした歯形です。（小原歯車工業発行　歯車設計支援ソフト　を利用）。転位に応じて歯元曲線の様子が異なっていることがお分かりかと思います。尚、小原歯車工業発行　歯車設計支援ソフト利用の歯形曲線はピニオンカッタ利用の歯形になっています。理由は不明です。

歯形のアンダーカット

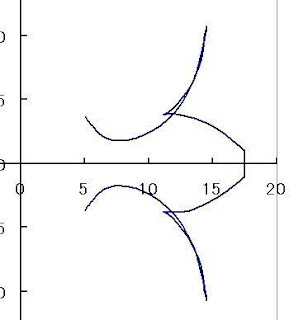
画像は当方で作成（構築）したインボリュート歯形曲線の方程式による切下げモデルの歯形をエクセルの散布グラフで表現したものです。歯数は５、転位係数０の条件で求めました(昨年１月頃のプログラムです。現在はプログラムを補正してあり、ここまでの表示はでませんが）。おおまかにいえば左側はトロコイド曲線、右側はインボリュート曲線になります。インボリュート曲線が左に流れて鋭角的に右側に反転するポイントは、本来切下げのない歯形の歯底曲線（トロコイド曲線）との交点すなわち基礎円上の位置になります。歯車の切下げというのはこの歯底曲線が歯形曲線（インボリュート曲線）側に食込んで歯形を削りとる状態を示しています。この図形を２ＤＣＡＤ上でヒゲの部分をトリミングすることで切下げされた実際の歯形になります。このトリミングに相当する操作を式の操作で行うことは極めて困難で、当方は数値演算で処理しています。この数値演算をＣ＋＋でプログラム化することは精度面（桁落ち対策など）で当方の力量では不可能に近く、エクセルの数値計算精度を信頼してエクセルＶＢＡで措置しています。切下げ歯形で実行時間がかかる理由がここにあります。それでも実際には歯数５枚では転位処理をしない限り当方の現在のシェアウエアのソフトでもこのヒゲの対策は解決できず、２ＤＣＡＤ上でトリミングして歯形を得ることになります。なお、この歯形モデルはラックカッタ（一般のホブ歯切り）によるもので、ピニオンカッタの歯形はトロコイド部の形状が少し変わります。この差異については次項で画像で説明します。歯底曲線が影響を受けるカッタの要素はカッタの歯先のＲ値（面取り状の半径値）によって変化します。カッタの歯先の半径が少ないほど歯底のトロコイド曲線のカーブがキツくなります。このアンダーカットを恣意的に採用する工夫も転位することで実際の設計には多く実施されています。当方のシェアウエアソフトでは現在、この伸びたヒゲはソフト修正の影響で画像よりは小さくなっています。

エクセルの散布グラフを利用した例

エクセルの散布グラフを利用して作成した歯車の噛合い図（一部拡大）です。これから回転の動的表示を試みましたが画面が揺れてうまくゆきません。Ｃ＋＋でなら可能です。縦と横の距離関係は極めて正確ですがＰＣの解像度設定によってはうまくゆかない場合があるかもしれません。（円が楕円で表示されるＰＣなど）

３点を通過する円弧の中心座標（ＶＢＡ）

平面上で３点を通過する円弧の中心座標を求めるプログラム例です。連立方程式の解法で行列演算を利用しているので、応用が利くと思います。

Sub テスト()

Dim A(1 To 2, 1 To 2) As Double
Dim B(1 To 2, 1 To 1) As Double
Dim I As Integer, X1 As Double, X2 As Double, X3 As Double
Dim Y1 As Double, Y2 As Double, Y3 As Double

With Worksheets("sheet11")
I = 1
Do
X1 = .Cells(I, 1)
X2 = .Cells(I + 1, 1)
X3 = .Cells(I + 2, 1)
Y1 = .Cells(I, 2)
Y2 = .Cells(I + 1, 2)
Y3 = .Cells(I + 2, 2)

A(1, 1) = 2 * (X1 - X2)
A(1, 2) = 2 * (Y1 - Y2)
A(2, 1) = 2 * (X1 - X3)
A(2, 2) = 2 * (Y1 - Y3)
B(1, 1) = (X1 ^ 2 - X2 ^ 2) + (Y1 ^ 2 - Y2 ^ 2)
B(2, 1) = (X1 ^ 2 - X3 ^ 2) + (Y1 ^ 2 - Y3 ^ 2)

.Cells(I, 6) = EquationAnswer(A, B)(1, 1)
.Cells(I, 7) = EquationAnswer(A, B)(2, 1)


I = I + 2
Loop Until I = 1101
End With
End Sub


Function EquationAnswer(ByVal A As Variant, ByVal B As Variant) As Variant
On Error GoTo ErrHndl
With WorksheetFunction
EquationAnswer = .MMult(.MInverse(A), B)
End With
On Error GoTo 0
Exit Function
ErrHndl:
EquationAnswer = CVErr(xlErrValue)
On Error GoTo 0
End Function

後記：尚、別の方法は下記ＵＲＬに記載してあります。
http://m-sudo.blogspot.com/2009/08/blog-post_3480.html

歯形曲線の円弧化

当方で作成済みで公開保留になっているソフトです。既に発行しているシェアウエアソフトを利用していることとその前提の上での歯形曲線の円弧化の長所の展望を持ちがたいために保留にしています。
現在、考えられる長所は円弧データであるために歯車の３Ｄモデル化に際してモデル容量が削減可能なことと円弧化によるＣＮＣ工作機への対応のしやすさが上げられます。尚、本ソフトのレベルで歯形の精度（数値）はほとんど誤差ゼロ（ミクロンレベル）といっても差し支えないほどです。

追記 2017.04.15
本機能は実は　Involute_Curve_3.1において実装されています。しかし、DXFデータ化が難しく、
この課題が解決するまで、隠しデータのままにしておこうということで、現在見えなくなっています。

油圧に関する計算

油圧に関する参考ＷＥＢからの画像です。上記画像の出典もここからです。リンクに記載しておきます。
http://www1.odn.ne.jp/yuatuy/index.htm
サージ圧に関する計算には作者の補正もされているようです。特にバルブの切換え速度などの影響は感覚でしか捉えようがなかっただけに実験式による補正がされているとすれば貴重です。

ブリガードの機構

画像は下記ＵＲＬ参照。角度θに対応したＰ点の座標値取得の画面です。
http://www.gctv.ne.jp/~kawakika/tricalc_brig.htm
この機構を眺めているとＰ点の位置をを一定範囲に押さえるためには１００の長さのリンク長の範囲など興味をそそる計算課題が想起されます。（１００の長さのリンクをシリンダなどで可変長リンクとする）
有償のソフトですが眺めていて損はないと思います。

FireFoxの利用

画像は、皆さまご承知かとは思いますが、私が普段利用しているインターネットブラウザのＦｉｒｅＦｏｘからのＧｏｏｇｌｅ検索画面です。私事ですが、検索をＧｏｏｇｌｅ主体の利用になってから、ブラウザをＦｉｒｅＦｏｘに切り替えました。ここのブログもＦｉｒｅＦｏｘの画面上で作成しているので、他のブラウザでは表示の不都合があるかもしれません。ブログ自体もＧｏｏｇｌｅ関係のアカウントから取得しているので他のブラウザのユーザー様には不便をおかけしているかもしれませんがご理解をお願いします。

引張りバネのリレーション駆動

Ｐｒｏ／Ｅ　2001　で作成した引張りバネのリレーション駆動モデルの例です。画像で下方の角度データを変更するとバネのピッチが変わり角度に応じた長さに変化します。画像の例では
Ｎ＝27.3183　　（＜＝＝(400^2+300^2-2*300*400*cos(180-110))^0.5/15）
d29:2=((d3:0)^2+(d2:0)^2-2*(d3:0)*(d2:0)*cos(d0:0))^0.5/N
ここでレバーの角度を１１０°から８０°に変更します。バネピッチが当初の15ｍｍから19.77に変わっていることがお分かりかと。アセンブリモデルでこの類のモデリングはバネだけではなくカム、リンク機構など様々な応用があります。リレーションの式の構築にちょっと高校数学の程度の応用力は必要とは思います。

動力伝達軸の設計＿２

軸の設計について。
もっとも困難なそして判断力の必要な設計は右の表でいえば｛回転軸（主軸を含む）｝でしょう。設計要素としてはかなり限定的で計算手順、方式も確立されているから意外に思われるかもしれません。しかし、機構のアウトラインを左右するものは駆動系の回転軸です。マンガでラフスケッチを描き、エクセルで計算式を構築しながら軸のデザインを決めてゆきます。
図の画像は下記ＵＲＬより
http://homepage2.nifty.com/ty-1999/kikaiyouso/jikunosekkei-01.html
ここのＵＲＬは軸設計の基本的なアウトラインを示しており、よくまとめられています。同じＵＲＬの別のページには段付き回転軸の計算方法が記載されています。
http://homepage3.nifty.com/mat/shaft.htm
ここのデータを｛動力伝達軸の設計＿１｝の計算式を参照しながら疲労強度を確認することで一応の信頼性のある設計が可能になります。ここで｛一応｝と記したのは、動力伝達軸の設計製作にあたっては実験検証が欠かせない性格の設計であると考える故です。実験が不可能な単品設計の場合は合金鋼の採用も視野に入れた十分な余裕のある設計が望ましいですね。（基本はＳ４５Ｃ、Ｓ５０Ｃなどでトラブルの生じた場合に合金鋼の採用という逃げ道を用意するなど。）

動力伝達軸の設計＿１

画像出典はhttp://www.rmc.mce.uec.ac.jp/より。この表に注目してください。材料の標準平滑試験片のデータは下記文献など参考にされてください。記載されているかどうかは不明ですが。

機械技術者・機械系学生必携の書　
　　　　平易な文章・わかりやすい解説図・豊富な演習問題！

「初心者のための疲労設計法」

日本材料学会疲労部門委員会発行　A4判124ページ
　　　　 定　　価　　　 1,250円（税込）
　　　　 会員特価　　 1,120円（税込）
　　　　 （送料：いずれも1冊につき380円，ただし10冊以上は無料）
さて、本題に戻ります。ロボットなどの超小型機構の設計にあたっては、全体重量、回転モーメントを少なくすることで軸径は極力抑える設計をします。応力計算では疲労限界に関する計算が欠かせません。本画像紹介のＵＲＬでは包括的な計算の概略が示されており、必要な設計計算の全体像が想定可能かと思います。本ＵＲＬに関しては設計：動力軸の設計計算としてリンクに記載します。

引張りバネの初張力について

追記：当方と全く同じ見解を示されています（画像以外の部分を含む）。実力のある設計企業と思います。普通はここまで踏み込んだ意見は述べないものですが。画像は下記ＵＲＬより引用しました。（以上、2009.04.15追記）www.takitard.com/spring.pdf

画像はＰｒｏ／Ｅで作成した引張りばねです。引張りバネの設計にあたって初張力を考慮しますが、この初張力を求めるには範囲を求めるグラフ線図が大概の引張りバネの文献に記載されています。そしてこの初張力の線図は加工後の焼鈍しを行わない状態でのデータであることです。普通はバネは若干の引張り強さは犠牲にしてもじん性を得る目的で焼鈍し処理を行います。この焼鈍し処理を行うと加工によって発生した残留応力を減少させることでばねの耐疲れ性を向上させます。この焼鈍しを行うと初張力は大きく損なわれます。従って焼鈍し処理を行って耐疲れ性を（じん性）得る必要がある場合は、初張力を
グラフ線図の下限以下にする必要があるかと思います。この設定はバネメーカーに問い合わせることで対応し、満足する結果の問い合わせ返信を頂いたバネメーカーに発注することが最適な対応でしょう。
さて、図のバネの最大の強度上の弱点はばねのフックとコイルの境目（フックの起点部）です。この部分の立体曲げ半径を十分に確保するようにしましょう。本稿はばね材料としてピアノ線を利用する場合の考察です。なお、圧縮ばねの場合は加工後の内部応力を除去する目的の焼鈍しを十分に行う必要があるので初張力の設定は意味を持ちません。

ロボットに関する考察

画像は
www.kawada.co.jp/technology/gihou/pdf/vol25/25_ron_12.pdf
より引用しました。ロボットといえば人に代わる動作を代替する機構体というのでしょうか。しかし、現在では動作というよりも動物体の模倣を機構的に完成したものをロボットといえるかもしれません。凡そ自然に存在したものを模倣できないモデルはロボットではなく単に自動機または自動機構と定義しても間違いないと思います。

その意味ではＨｏｎｄａ技研工業のアシモは人型を追求しているロボットといっても私には違和感はありません。さて、紹介する図は恐竜モデルのロボット化の試みの一端を示しています。このＰＤＦのアウトラインにはロボットとは何？を問いかけてくるプレッシャをいつも痛感しています。動物の進化段階での早期の状況の解析はもしかしたら、基本的なというか、何か根源的な命題の解決につながるかとも思います。人とは異なる円滑な２足歩行モデルの可能性など。本稿の目的はロボット設計での基本的な考察（ラフスケッチ：基本構想設計）の参考になるＵＲＬとしての紹介が主眼です。

Ｗｏｒｍ の モデリング（Ｐｒｏ／Ｅ）

当方のＢＢＳに記載されているデータ。このテクをご教授頂いた方には深謝あるのみです。
画像は２条ウオーム。