ソフト紹介：楕円積分計算ソフト

本ソフトは、技術上の難点があり、プログラムに関心を持たれる方には有償2,000円にて、プログラムコード公開版の譲渡が可能です。C++でも試してみたのですが、誤差がひどくてかないませんでした。Excel計算の凄さを実感しました。使用したロジックはガウス・ルジャンドル法です。シンプソンの積分法ではここまでの精度確保は不可。（ガウス・ルジャンドル法の場合、最適の積分点数を推測することが重要だが、1500個レベルになると演算誤差の蓄積で帰って、精度が落ちてゆきます。）

1500個レベルで、最も高精度の数値を算出します。2015.01.22記。

プログラムコード非公開版は下記よりダウンロード可能です。（無償）

http://m-sudo.blogspot.jp/2015/01/gausslegebdrequadraturexls.html

 第一種楕円積分：小数点以下１４桁の精度はごく一部を除いて確保されている。

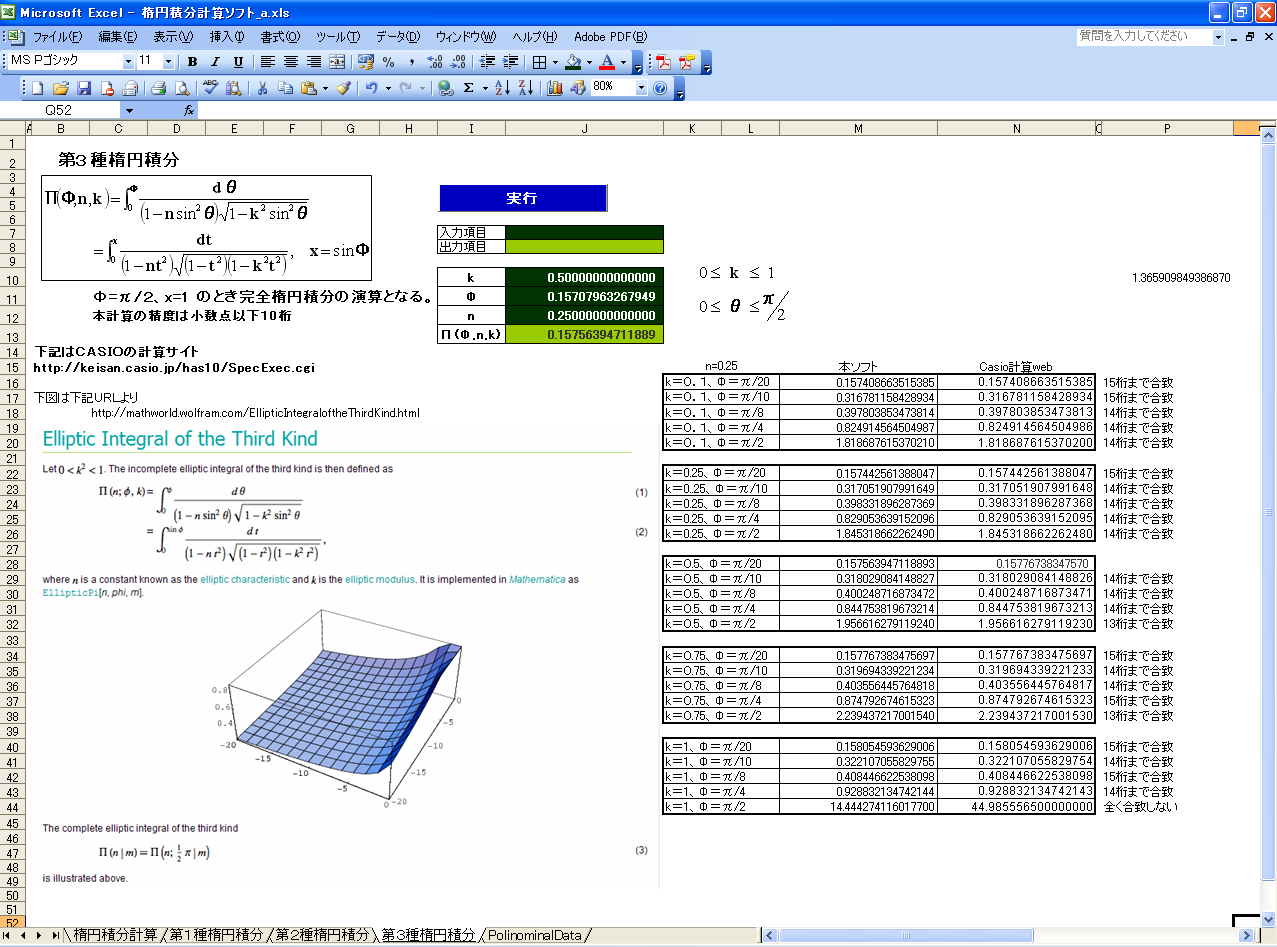
第二種楕円積分：小数点以下１４桁の精度は確保されている。楕円の部分弧長の正確な算出には必須です。

第三種楕円積分：角度がπ/2に近づくと誤差が大きくなる傾向がある。ｎ値によってはどのように変化するか、全く不明。現在検証中。n値が0.25以下の場合は角度がπ/2に近づかない限り小数点以下１3桁は確保。精度とパラメータの関係に関心のある方には解決策を相談したいところです。

追記）2015.01.22　

PCをより高速マシンに変更することによって、積分点数1500個のデータ算出がすばやく表示可能になったので計算をやり直したところ1500個で予想以上の精度が確認できました。