英語図面の読み方・書き方講座

企業向け講座（個人でも受講可能と思いますが、費用が高いので。）
http://www.nikkansc.co.jp/semi_pdf/eigozumen150423.pdf

JIS 溶接記号の DXF データ

標記の件、下記からダウンロード可能にしました。
もともと、登録していたのですが、サーバーの中身を変更した際に、抹消してしまったのに気がつきませんでした。JIS2010の改正を加えて再登録しました。
http://m-sudo.sakura.ne.jp/soft_data/AutoCAD_LT_2000_data_base/Welding_data_1.zip

旧JISからの更新は不完全かもしれません。
データはAutocad LT 2000　DXFデータという旧いCADで作成してあります。

接触応力：円軌道上の球体

画像は下記Webより
http://www.amesweb.info/HertzianContact/ContactStressesSteelBallBearing.aspx
設計への実際の適用も上記Ｗｅｂを読まれたうえで実施してください。
引用文献は野心的な（先進的ともいうべきか）内容のようです。著者は、ピーターソンの集中応力に関する著作もあります。

参考：http://www.amazon.com/gp/product/0471032212/ref=as_li_tl?ie=UTF8&camp=1789&creative=9325&creativeASIN=0471032212&linkCode=as2&tag=ameswebinfo-20&linkId=KUYNHNUWECP7DVIQ

追記)2015.01.31
上記図書は高価ですが、購入して損はないと思います。（企業として購入の場合。）

パルスローラー：協和製作所

以前、一度紹介済みだが、設備設計に欠かせないアイテム。電気制御の知識が必要だが、この程度の駆動回路設計の知識は、現役の設計者には常識でなければ、エンジニアとして通用しない。しかし、カタログを眺めると、至れり尽くせり、で、必要な知識もなくてもできそう。
http://www.kyowa-mfg.co.jp/05_catalog/pdf/prs/pr_all.pdf

他にモーターローラーもある。
http://www.kyowa-mfg.co.jp/05_catalog/pdf/ac_mr/mr_all.pdf

低燃費タイヤの開発｛よく転がるのによく止まる｝：ブリヂストンタイヤ

車の低燃費タイヤに関する記事。

http://jbpress.ismedia.jp/articles/-/42711

相反する事象に絶対はない、両立させた技術の最前線（ブリヂストン小平工場）での話。ブリヂストン小平工場の設計棟の応接フロアーにはタイヤのモデルが置かれてあった。十数年前に超高速回転するタイヤの内面観察装置の受注案件で寄ったことがあった。受注には至らなかったが（別に難しい件ではなくて街の設計屋さんならこなせるレベル。）そんなこともあってちょっと気になった記事です。

北極くま（白くま）の収容展示施設（モスクワ）

画像は下記Ｗｅｂより
http://urspolar.exblog.jp/20810925/
まだ成長途上の白くまとのこと。広い清潔感のある北極熊収容施設ですね。国内では、札幌の円山動物園、大阪の天王寺動物園で昨年暮れの赤ちゃん誕生が話題になっていますが、一度自然に近い環境で眺めてみたいものです。
画像からロシアの婦人（左端）と白くまの大きさを比較できそうですね。広角レンズの特性なのか知らないけれど、くまの足の太さと婦人の胴回りがほぼ同じに見えてしかたがない。（白くまは５歳、人間でいえば１５歳ころかな・・・）

久しぶりに文献購入：Theory of Plates

久しぶりに文献を購入しました。昨日発注。購入価格は、画像と異なり、配送費込で4,303円（新書です。）Amazon利用です。改めて、平板の曲げ理論を基礎から学び直そうと思いました。（実は、当方の計算法の思い込みのチェック用です。）Amazonの利用は、紀伊国屋や有隣堂経由より半額以下で購入の可能性があるので重宝します。他に、横浜の本店へ行く手間も不要。八王子のくまざわ書店では、欧米の科学技術書籍が１０年近く以前は置かれていたのだが、現在は見当たらず、時代の流れを感じています。有隣堂に関しては、青山学院大学理工学部が、近所に越してきたので、関連支店も近くにあるのですが。）
もう一つの狙いは、円板のたわみ式の詳述を学びたいことです。（国内の文献には、図表利用式が主体のため。下記のような式がどこから得られるか導出を確認するのが主目的。IT上のWebより得られたので。）

上記紹介の書籍ではありません。円板の場合は積分計算のC値を求める論理が判明しているので、式の確認で済むかな・・・と思います。（甘いかもしれないが）
追記）2015.02.11
上記関連データ計算式をｐｄｆにまとめたファイルを公開します。海外の文献です。誤植、考え方の過ちなど疑問の多い文献が横行しているので、本データの計算式はよく吟味のうえで使用してください。間違いの可能性も十分あります。
http://m-sudo.sakura.ne.jp/soft_data/kikaisekkei_data/Enban_Tawami.pdf
出典元はご希望の方はE-mailにて。

ばねの設計資料（英文）

このようなデータも存在する。重ね板ばねの設計資料を探しているうちに見つけたもの。1944年刊行ですが、ばねに関する公式の由来を示す文献として有用と思われます。応力修正係数で著名なワールの名前が・・・
https://webfiles.uci.edu/dbeerer/lit/Mechanical%20Springs%20Wahl.pdf

下記はUSAの大学教育用資料　ばね設計関連
こちらは現代のデータ
http://nptel.ac.in/courses/112105125/pdf/mod7les1.pdf
http://nptel.ac.in/courses/112105125/pdf/mod7les2.pdf
http://nptel.ac.in/courses/112105125/pdf/mod7les3.pdf

下記はばねの全体的なまとめ（セミナーの説明用資料）。眺めるだけで十分。

http://fs-server.uni-mb.si/si/inst/iko/lsek/obvestila/spring_seminar_presentation.pdf

ソフト紹介：Gauss_Legebdre_quadrature.xls

高精度数値積分演算　ガウス・ルジャンドル法の積分点データを算出するソフトウエアの紹介。
実用上積分点数1200前後の数値は14桁の精度を保持しています。演算そのものは2000点以上でも計算しますが、1400点あたりで、誤差が出現するような気がしています。Casioの計算サイトには見つからないので重宝すると思います。VBAのプログラムコードは公開しています。Alt + F11　で覗くことが可能です。　
下記リンクでダウンロード可能です。(無償：著作権は当方保持。）
http://m-sudo.sakura.ne.jp/soft_data/kougyou_suugaku/Gauss_Legebdre_quadrature.xls
Zip圧縮しないとソフトが壊れてしまうことを失念しました。下記でダウンロード可能です。
http://m-sudo.sakura.ne.jp/soft_data/kougyou_suugaku/Rujyandoru_no_Takousiki_kai_keisan.zip
本ソフト作成にあたり、下記Webにお世話になりました。
http://homepage1.nifty.com/gfk/Gauss_Legendre.htm

積分点データの検証に下記Webを利用させていただきました。
http://www17.ocn.ne.jp/~lite/
楕円弧の長さ　の項
このサイトではフリーの２D-CAD　Jww で描画した図形の断面２次モーメントを求める方法も紹介されています。

ちょっと気になることがあり、積分点数1500で計算をしてみました。

N=1500で最強の結果がでました。

N=1500の計算はDell Precision T3500機に変えて、5分ほどで結果が表示。

以前のPC（Dell　Precion)では3時間ほど要していたのですが・・・・。

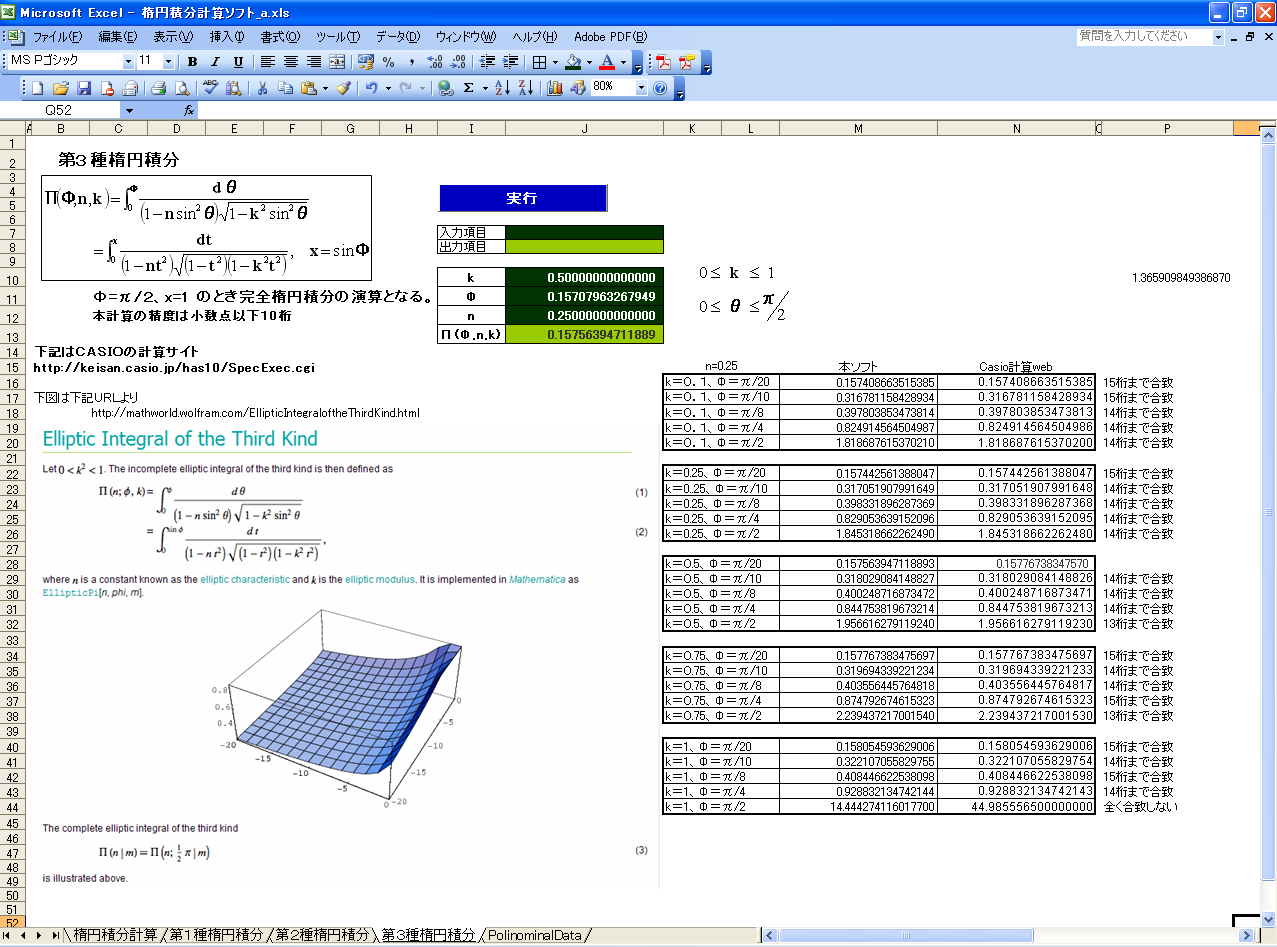
ソフト紹介：楕円積分計算ソフト

本ソフトは、技術上の難点があり、プログラムに関心を持たれる方には有償2,000円にて、プログラムコード公開版の譲渡が可能です。C++でも試してみたのですが、誤差がひどくてかないませんでした。Excel計算の凄さを実感しました。使用したロジックはガウス・ルジャンドル法です。シンプソンの積分法ではここまでの精度確保は不可。（ガウス・ルジャンドル法の場合、最適の積分点数を推測することが重要だが、1500個レベルになると演算誤差の蓄積で帰って、精度が落ちてゆきます。）

1500個レベルで、最も高精度の数値を算出します。2015.01.22記。

プログラムコード非公開版は下記よりダウンロード可能です。（無償）

http://m-sudo.blogspot.jp/2015/01/gausslegebdrequadraturexls.html

 第一種楕円積分：小数点以下１４桁の精度はごく一部を除いて確保されている。

第二種楕円積分：小数点以下１４桁の精度は確保されている。楕円の部分弧長の正確な算出には必須です。

第三種楕円積分：角度がπ/2に近づくと誤差が大きくなる傾向がある。ｎ値によってはどのように変化するか、全く不明。現在検証中。n値が0.25以下の場合は角度がπ/2に近づかない限り小数点以下１3桁は確保。精度とパラメータの関係に関心のある方には解決策を相談したいところです。

追記）2015.01.22　

PCをより高速マシンに変更することによって、積分点数1500個のデータ算出がすばやく表示可能になったので計算をやり直したところ1500個で予想以上の精度が確認できました。

形鋼データベース＿DXFデータ

形鋼データベースの展開例
下記Webから入手可能です。
http://m-sudo.sakura.ne.jp/soft_data/AutoCAD_LT_2000_data_base/Katakou_dxf_de-ta.zip

追記）2015.01.19
形鋼、ボルトなどの形状、重量データ、塗装面積など掲載されているデータ集は下記。
(ファイル内にパスワード情報も含まれています。）
http://m-sudo.sakura.ne.jp/soft_data/kikaisekkei_data/ryousen_enziniazu_katakou_de-tabe-su.zip

このデータは予告なく抹消される可能性があります。このデータの紹介に関しては下記ページを参照。
http://m-sudo.blogspot.jp/2014/06/exe.html

開発ソフト紹介：３次、４次方程式の解を求める

３次、４次方程式の解を求めるソフトの画面。解が高精度である故に、解の範囲を狭くして解の様子を調べることも可能です。本ソフトはフェラーリの解法を忠実になぞって計算しています。
参考：http://www.wakayama-u.ac.jp/~chen/download/equation/equation.pdf

当方作成の歯形作成ソフト Involute_Curve_3.1 において、歯形係数を求める演算中、歯元曲線の３０度接線の接点位置を求める計算で、３次方程式のサブルーチンを利用しています。

縦弾性係数とポアソン比_データ作成

過去に作成したブログからデータを抽出し、pdfデータを作成しました。
下記URL参考。
http://m-sudo.sakura.ne.jp/soft_data/kikaisekkei_data/Jyudanseikeisu_Poason_hi.pdf

当面、過去の設計データをまとめる作業を優先します。

追記　2016.03.14
本ブログの縦弾性係数に関する過去のページは全て削除しました。縦弾性係数に関するデータが必要な方は上記リンクからｐｄｆデータをダウンロードしてください。
ＩＤ，パスワードは下記リンクに記載があります。
http://m-sudo.blogspot.jp/2016/02/htaccess_20.html

静摩擦係数、動摩擦係数、転がり摩擦係数のデータ集

表記のデータ集を現時点でまとめてみました。ご利用を考慮される方は下記URLからダウンロードしてご利用ください。（PDFデータです。）

http://m-sudo.sakura.ne.jp/soft_data/kikaisekkei_data/Masatukeisuu_de-ta_syuu.pdf

断面性能に関するデータ集（断面積、断面2次モーメント、断面2次半径、断面乗積、慣性モーメント）

表題のデータ集をまとめました。内容に重複がありますが、本ブログでの当面の最終データ集です。
http://m-sudo.sakura.ne.jp/soft_data/kikaisekkei_data/Danmen_Tokusei_ni_kansuru_de-tasyuu

成形歯車の場合の歯形曲線（歯元半径）の策定の特許

http://www.fa-navi.jp/patent/details/000686322.html#

ここのWebにおいて歯形（歯元曲線）に関する特許の説明が掲載されています。

当方の Involute_Curve_3.1では、バックラッシの歯厚減少量に対応した歯形曲線の一筆書きデータ、および歯形係数の高精度の策定が可能です。本ソフトに記載されているワイヤーカット加工モードは、上記特許文書の成形歯車の規定を抱合していると思います。但し、当方のソフトは噛み合いに忠実になぞったトロコイド曲線を歯元曲線として採用しています。

(続々）歯形噛み合い状態描画ソフト：Involute_Gear_Gearing_Data

前、前々ページの説明　歯先の干渉、不干渉の様子を比較表示してみました。20の数字は目盛り（mm）です。画像は拡大表示です。図示の使用ソフトは5,500円で利用可能です。ご希望の方はE-mailにてご連絡をお願いします。

(続）歯形噛み合い状態描画ソフト：Involute_Gear_Gearing_Data

前のページで歯先の丸み係数を0に近似させて（0.001：0にすると分母が0の演算でエラーが生ずるために0.001で代用）描画してみました。

干渉がなくなり、心持ち隙間さえ見えると思います。前ページのデータとは工具歯先の丸みをゼロに近似させた以外はすべて同一条件です。

歯溝部の形状がかなり尖鋭化しているのがお分かりと思います。

工具歯先の丸み係数が0.375のとき、歯車の歯先に1.875の丸み (0.375*5=1.875)を設定することでも干渉は防げますが、当方のソフトは歯先の丸みの設定は行っておりません。（代わりに面取りを可能にしています。）

歯形噛み合い状態描画ソフト：Involute_Gear_Gearing_Data

噛み合う歯車の噛み合い状態のコマ送り状態描画ソフトの表画面。頂げきゼロに注目。コマ送り描画画面はSheetに描かれ、20コマ回転順に並んでいる。
Involute_Curve_3.1に付属。廉価版には付属しない。
キーワード：噛み合い　噛み合い率

青色歯車が時計廻りに駆動している。

歯先が干渉気味になっているが、間違いではない。本ソフトの歯形はラックカッターで創成したデータであり、ラック工具の歯先丸み係数0.375を織り込んでいるために干渉する。丸み係数をゼロにすると隙間が生ずるはずである。この隙間はラックカッターの歯先幅寸法がピニオンの歯先幅より小さいことによる。

通常は頂げき係数1.25または（研削、シェービング歯車の場合）1.35の設定によって十分な隙間がとられている。画面の20は20mmの目盛を示している。

この一連の噛み合いの様子は歯車ポンプの効率を考察するうえで、十分参考になる。

Involute_Curve_3.1_Excel2010 Edition

Excel2010 (Windows8.1）版　Involute_Curve_3.1 の画面。以前のバージョンも同様にリフレッシュしました。旧正式版購入者に、プログラムコードのロックが完了次第送付予定。（ロックの方法が意外と難しい。）歯形描画に関する必要事項はすべて織り込み済みです。他にかみ合い状態コマ送りソフトも同梱します。旧版をお持ちの方はフォルダーを別にしてファイルしておく必要があります。DXFデータの出力格納位置は旧版と共通です。（Cドライブ直下）

本ソフトの歯形はラックカッター創成歯形でピニオンカッタ創成歯形には対応していません。一度で描画可能な歯数は６枚。５枚以下はCAD操作でトリミング作業が必要になります。（ただし、３枚以上）転位歯形は歯車理論そのままの軌跡を一筆書きで描画します。

歯形描画にバックラッシに対応した歯形描画が可能であり、対応する歯形係数、またぎ歯厚、オーバピン径　及びそれら許容値に対応した歯形出力が可能です。（またぎ歯厚許容値のみ近似値です。）

歯元の丸みはラックカッターをなぞる特殊な曲線を描きます。但し、こぶつきラックカッター歯形には対応しません。

譲渡価格は、５，５００円。　

キーワード：歯形係数　噛み合い率　頂げき　バックラッシ　またぎ歯厚　許容値　オーバピン径　転位

人体模型データ：視野範囲

詳細な人体模型例：視野範囲
出典は画像に記載
http://www.arch.mcgill.ca/prof/castro/arch304/winter2001/dander3/frame/ergonomics3.gif

過去の紹介ブログにも追加記載しました。
http://m-sudo.blogspot.jp/2012/11/blog-post.html

歯形係数のグラフ

上図右のグラフは下記Webより。
http://www.ecs.shimane-u.ac.jp/~shutingli/CADgeardesign3.pdf#search='%E6%AD%AF%E5%BD%A2%E4%BF%82%E6%95%B0'

---------------------------------------------------------------------------------

追記 2017.04.17

下図は日本機械学会の歯形係数の計算式を示している。ただ、日本では日本歯車工業会が適切な計算式を呈示している。

但し、日本機械工学会の算式の採用はより安全側に入るのですが。だからといって、これでよしというわけにはゆかない。

日本歯車工業会呈示の歯形係数算式は下図。　この計算式を利用しなければならない。

---------------------------------------------------------------------------------

下図は当方の計算ソフト(Involute Curve3.1より)

最上段右のグラフは、JGMAではなくて、なにか、別の理論で計算されたデータではないだろうか。数値が全般的に低いので、もしかしたら、航空機関連の歯車強度理論に沿っているのではないだろうか、などと、想像してしまう。一般の機械部品としての数値の採用は危険と思いますが。
数値の差は近似値として”同じ”とはとても言えない差になっています。

数年前にこのブログで指摘しておいたのですが。
http://m-sudo.blogspot.jp/2012/11/blog-post_3367.html

LUG強度計算（航空機用）の資料のダウンロード

出典：

http://files.engineering.com/download.aspx?folder= 4c02ebf3-6425-478f-86c7-a73390725bf8&file= Air_Force_Lug_Analysis_(section_9)%5B1%5D.pdf

段付き軸 徐変断面軸の座屈強度計算式データ

表題の計算式データをPDFにまとめたので，必要な方は冒頭の文章を熟読の上で、活用されてください。全２４ページです。

http://m-sudo.sakura.ne.jp/soft_data/kikaisekkei_data/Dantukijiku_Jyohendanmenjiku_zakutukeisansiki.zip

スーラ 「グランド・ジャッド島の日曜日の午後」(1884～1886）

スーラの作品はサーカスを描画したデータを過去に紹介したが、この作品もまたスーラの代表的な点描画といわれる。データが jpeg データなので原画の趣は薄れてしまってはいると想像するが、点描画の趣は残していると思う。シカゴ美術館蔵とのことだが、シカゴ美術館へ行った当時はスーラのことは何も知らなかった。記憶にないのである。
サーカスの紹介画像は下記。
http://m-sudo.blogspot.jp/2011/04/blog-post_2786.html

昨年暮れから新年３日まで絵画の紹介の寄り道をしたが、明日からはまた、機械設計のテーマに戻ります。
日本製紙系　NPI関連のカレンダー(2015)より。

現代の絵画作家作品：花市、マドレーヌ広場 ミッシェル ドラクロア

現代フランスを代表する画家、ミッシェル　ドラクロア(1933～）の作品　｛花市、マドレーヌ広場｝
大和証券カレンダー（2015）より。　Epson ES-8500　24bit  600dpi
過ぎしある時代風景の描画。メルヘンチックな雰囲気を描く作風かもしれない。

あけまして、おめでとうございます。

あけまして、おめでとうございます。今年のブログスタートは、USA,シカゴ美術館蔵の欧州印象派を代表するカミーユ・ピザロの作品：パリ、ル・アーブル広場（1893）の紹介です。シカゴ美術館へは２０年近く前に行っており、ピザロの作品が何点か飾られていました。１９世紀のパリの雰囲気をよく描写している作品です。この雰囲気の醸し出す空気の香りの描写に印象派の強烈な存在感があるように思えました。

JX日鉱日石エネルギー社のカレンダーより。EPSON ES-8500 24bit color 600dpi