数値解析：ガウス-ルジャンドル法

シンプソンの式と並んで積分の数値計算に利用されるガウス-ルジャンドル法に関する説明サイトの画像。
引用は下記URLより。
http://www17.ocn.ne.jp/~lite/
ここで注目するべきは、積分点の重み係数の算出方法の説明。大変貴重なサイトです。
計算しなくてもデータを得るというのであれば下記画像から求めることができます。
これも上記URLより引用しました。
追記：後日検討した結果、上図の説明はあまり薦められない。連立方程式を利用することで誤差が積重なり
１０個ほどの積分点で不正確な数値になってしまうので信頼性がおけない。別の方法で当方で下記URLにて最新の積分点をもとめるソフトを公開しました。Excel VBAで有効数字14桁の精度があり、2000点以上の積分点、重み係数も有効数字14桁の精度があります。09.09.09　記　（14.12.05修正)

http://m-sudo.blogspot.com/2009/09/blog-post_528.html




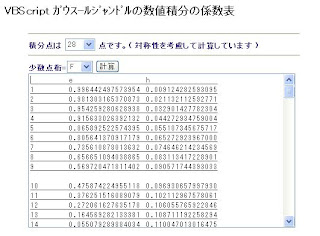
小数点以下２０桁までのデータは下記。
引用は下記URLより
http://math.fullerton.edu/mathews/n2003/GaussianQuadMod.html


尚、積分点の数値そのものをプログラム（VBA)で求める場合は下記画像が参考になります。


上記画像は下記URLより。　有限会社　ゴッドフット企画
http://homepage1.nifty.com/gfk/Gauss_Legendre.htm
ここの別の箇所に重み係数を求めるVBAコードが記載されていますが、このコードのプロセスが私には全く理解できないので、重み係数に関する算出プログラムは先頭の画像の説明から自作する方がよいと思います。

追記：ここのコードのプロセスがやっと理解できました。拠って紹介のコードを一部修正(コードの抜けを埋める）のうえで編集作成したソフトをフリー（コードを含めて完全公開版）で公開しました。下記URL参照。
http://m-sudo.blogspot.com/2009/09/blog-post_6811.html