機械設計に関する情報を紹介してゆきたいと思います。 このブログの過去の記述は、画面左上の空欄に、例えば、油圧、と記入すると関連する記事が現れてきます(2文字以上)。Googleの設定の仕様の変化に対応して自動的に画面の配置の仕様が変更されますが、基本的な変化はありません。神奈川県横須賀市森崎5丁目付近のグリーンヒルケアハウス在。
counter
2013/02/26
楕円歯車を構成する計算式:楕円インボリュート曲線
上図は下記URLより
http://mathworld.wolfram.com/EllipseInvolute.html
なんと楕円インボリュート曲線関数を記述するウエブを見つけてしまった。楕円歯車に関する厳密な式の記述には、平行曲線、歯底曲線(ラックカッターの軌跡)の方程式が必要になる。楕円積分計算のソフトは作成してあるのでサブル-チンとして利用することで楕円歯車の大枠は形成できる。
尚、別のページでは下記記述がある。
下記URLより。
http://m.wolframalpha.com/input/?i=ellipse+involute&x=6&y=10
追記:よく考えて見ると、歯形データ取得には高いハードルがある。基礎円に相当する基準楕円をベースに考えると、ピッチ楕円弧、歯先楕円相当弧はすべて、基準楕円の平行曲線でしかない。厳密に言う楕円とは異なるのである。しかし、それなりに歯形のプログラムのコード化は可能だろう。歯元曲線の曲線形状は円の半径で代用するしか方法がないかもしれない。
2013/02/23
曲がり梁:曲げ中心-中立軸 間の距離計算
画像は曲がり梁の曲げ中心~中立軸間の距離(Rm)を求める方法。この図では四角形断面の例ですが、様々な断面形状にこの考え方が適用できます。
図中のRm=A/AmはRm = Σ(A)/Σ(Am)の考え方でよく、複雑な形状は単純な形状の組合せで計算が可能になります。減算操作も可能なので上図の例からは角形中空断面の計算が容易に行えます。とはいえ、積分演算は煩雑で、参考文献の公式を利用することが無難になります。
参考URL:http://m-sudo.blogspot.jp/2013/02/blog-post_17.html(応用例)
http://m-sudo.blogspot.jp/2013/02/web.html(公式集)
上図中、e は図心(断面)と中立軸(曲がり梁断面)間の距離。
( e = R - Rm )
追記)曲がり梁の形状係数を求める公式集
http://m-sudo.blogspot.jp/2014/03/log-post_4.html (2014.12.02 記)
2013/02/20
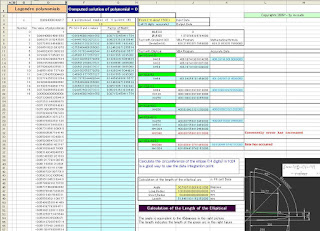
楕円に関するデータ計算ソフト
上図は拙作の楕円に関するデータを求めるソフトの主画面です。本来は楕円歯車のモジュール策定計算と歯のピッチ角それに関する基礎円径(楕円の場合、周上の位置に応じてデータが変化します。)を求めるために作成しました。
別シートにはガウスレジャンドル法の積分点データを求めるソフトを用意しています。このデータの活用の仕方によっては、かなりイビツ、または、極めて真円に近い形状の楕円データも高い精度で求めることが可能になります。
本ソフトは、現在、Involute_Curve Ver3.1 の購入者に無償で送付しています。近い将来には機能を改善の上で、有償化(頒布予定価格:5,500円)も視野にいれています。
2013/02/18
風力発電に関するガイダンス(英文)
上図は10年以上も以前に公開された風力発電の発電機に関する小冊子の一部。今からでも風力発電に関わる開発は遅くはないので、基礎から学び直すのもよいかもしれない。本冊子の内容は下記URLからダウンロード可能です。
http://m-sudo.sakura.ne.jp/soft_data/
下記赤枠内のデータ。
http://m-sudo.sakura.ne.jp/soft_data/
下記赤枠内のデータ。
2013/02/17
工夫:曲がり梁の計算
上図の引用元URLは下記。
http://site.iugaza.edu.ps/marafa/files/Analysis-of-Curved-Beams.pdf
図中、コメントで示したが構成部材の曲がり梁の計算例に示されるように曲げ中心からの断面中立軸半径(R)を求めるにあたっては、構成部材の加減算が適用できる。中空部材(丸パイプ、角パイプなど)の計算にはこの考え方が便利である。
http://site.iugaza.edu.ps/marafa/files/Analysis-of-Curved-Beams.pdf
図中、コメントで示したが構成部材の曲がり梁の計算例に示されるように曲げ中心からの断面中立軸半径(R)を求めるにあたっては、構成部材の加減算が適用できる。中空部材(丸パイプ、角パイプなど)の計算にはこの考え方が便利である。
2013/02/16
ソフト紹介:3次、4次方程式の解を求める
2013/02/12
2013/02/11
曲がり梁の計算_Webデータより
追記)2015.07.11
下記画像データが小さくて見えがたい場合は、画像をマウスでクリックして、ペイント画面に貼り付けてください。見やすくなります。
上図は各断面形状に応じた曲がり梁の曲げ中心から図心、中立軸までの距離を求める式。
これらの式をどのように利用するかは下記問題例を参考にする。
問題例
問題例
上図は下記URLより引用し、データの体裁を改修したもの。他にも問題例が詳述されている。
http://c501400.r0.cf2.rackcdn.com/documents/mechanical/Curved%20Beam.pdf
2013/02/10
曲がり梁の形状係数_K
 |
| 角パイプ、形鋼など部材の幅寸法に特殊な条件を設定しているが、Roark’s Formulas (7th Edition) には極めて煩雑な式が記載され、簡略的には本表と同じ条件を記載した表が併記されている。本図はこの文献の表を利用して作成されたように思える。 |
http://www.eng.uah.edu/~wallace/mae466/DOC/bas_str.pdf
三角形、台形、逆三角形、逆台形に関しては下記URLを参照。
http://m-sudo.blogspot.jp/2013/04/blog-post_9.html
曲がり梁の概略計算には上記グラフを利用することもひとつの方法。
曲がり梁の各種断面の中立軸と中心軸の曲げ中心からの距離を求める表データは
下記URLに詳細に記載されている。
http://c501400.r0.cf2.rackcdn.com/documents/mechanical/Curved%20Beam.pdf
上図データは当方のデータサーバーに格納済み。
ファイル名はCurved Beam.pdf
データサーバーのURLはhttp://m-sudo.sakura.ne.jp/soft_data/
このpdf データはとても貴重なので次のページにて紹介します。
過去に同様の投稿を行っていました。こちらのURLの内容を優先してください。
http://m-sudo.blogspot.jp/2012/06/blog-post.html
インボリュート歯車の噛み合いの様子
拙作の自作ソフト InvoluteGearCurve Ver3.1とその付属ソフト InvoluteGear Gearing Dataを利用して歯車の噛み合いの様子を描画してみました。噛み合いの正確さを強調するために、片方の歯車の歯数は6枚として、バックラッシゼロ、頂げきゼロの状態で描画しました。
 |
| 歯車データ数の設定 |
 |
| 頂げき係数の設定 |
 |
| 歯車の仕様 |
 |
| 噛み合い描画のための手順説明 |
 |
| 噛み合いのコマ送り状態描画ソフトの操作直後の画面 下方のシートが状態描画を指している。 |
NCフライス盤を利用した高精度歯車歯形の作図法 塚元尚久(千葉工業大学)、百瀬一久(旧ヤシカ岡谷工場) 昭和52年11月。
この論文を掲載した雑誌記事は、文章、図など誤植が多く、基本的な数学公式しか信用できなかった。以下噛合い状態のコマ送りデータ。(エクセルの散布図で作成しているので拡大表示が効きます。)本ソフトの購入申し込みはブログ右のプロフィールよりE-mailにてご連絡ください。
(価格5500円)
 |
| 1/20:噛合いの開始 |
 |
| 2/20 |
 |
| 3/20 |
 |
| 4/20 |
 |
| 5/20 |
 |
| 6/20 |
 |
| 7/20 |
 |
| 8/20 |
 |
| 9/20 |
 |
| 10/20 |
 |
| 11/20 |
 |
| 12/20 |
 |
| 13/20 |
 |
| 14/20 |
 |
| 15/20 |
 |
| 16/20 |
 |
| 17/20 |
 |
| 18/20 |
 |
| 19/20 |
 |
| 20/20 |
2013/02/07
近頃の記事より:液晶用高画質フィルムの開発
http://sankei.jp.msn.com/west/west_economy/news/130205/wec13020518520009-n1.htm
同じく
http://sankei.jp.msn.com/west/west_economy/news/130204/wec13020410170001-n1.htm
慶応大学の小池教授といえば光ファイバー関連の開発で名前を知られていますが、氏の名前に信頼感を抱くので確実なニュースといえます。
登録:
コメント (Atom)