枕草子より現代へ・・・

http://jbpress.ismedia.jp/articles/-/44350
この著者の他の作品にも注目してみたい。

是非導入しておきたいソフト：Adobe_Acrobat_Professional 最新版

表記のソフトは金額にして6万円近くはする高価格のソフトである。PDF関係では、フリーソフトも含めて多々、存在するが、制約が多すぎる。中途半端な有償ソフトは購入する価値がない、というのが、実感である。しかし、機械設計エンジニア（個人経営など）にはCADデータのPDF化など必須の機能がある。期間契約でもよいかもしれないが、購入がおすすめである。最大の威力の発揮は、WebのPDF化と思われる。PDF資料中の画像データなどはクリックすることで明瞭なデータが導入できる。
当方のブログ縮小への対応は

１）各テーマブログのPDF化印刷処理。
２）PDF化印刷処理したPDF画面から画像データをクリック。その画像データをPCにファイル。

上記でOK。AdobeAcrobat　Professional の最新の正規版にのみ対応。

転がり軸受け構成事例集：ドイツFAG社発行の文献

ドイツFAG社の公開文献（英文）　全200ページ
http://www.schaeffler.com/remotemedien/media/_shared_media/08_media_library/01_publications/schaeffler_2/publication/downloads_18/wl_00200_6_de_en.pdf

WebページのPDF化の方法

Google Chrome を使用して作成したPDFファイル。

ASME 機械製図 規則（2010）：Web より

当方の旧PCから見つけ出した文書。公的な市民講座のような場で支給される文書と思われる。どこから見つけ出したかは現在は不明。（Webより入手)
下記より入手可能（全24ページ)。
http://m-sudo.sakura.ne.jp/soft_data/kikaisekkei_data/CADdeptStandards_ASME.pdf

過去ブログの削除について

過去のブログについて、ITの検索から直接ブログへ寄ることの利便性の廃止を現在、最優先課題と考えています。必要な方はサーバーのデータを自力で検証してくださるようお願いします。また、過去のブログがすべて生き乗るわけではありません。（今夜から対策を実施します。）

今後のブログの方向

本ブログにお立ち寄り頂きありがとうございます。本ブログを開設して来年は９年になろうとしています。開設して１０年経過したらどうしようか、と。時折に考えていたりしますが、そろそろ、紹介記事の軽量化を図ってゆこうかと思います。
基本的には　
文献データは（Ｗｅｂデータを含む）削除してゆく。
本ブログは当方作成のソフトウエアの紹介記事に特化してゆく。
新規にデータの紹介は縮小する、もしくは新規紹介は中止してゆく。
上記３点の方向性が主体になります。
当方のサーバーは残しますが、記載データは削除の方向に軸足を移し、将来的にはサーバーの廃止も考えます。サーバーの維持費が年間２万円近いので、ソフトの販売収入では維持できない事情をご了解お願いします。
現在、痛感していることは、機械工学関連の文献が書店から見えなくなっていること。
以前から、設計情報が、書籍を通じて得られる状況が、国内では、極めて貧弱であることは知っていたのですが、間違った(間違いに近い）情報が書籍を通じて拡散されることさえ、散見されている国内の実態が存在します。さらにいえば、著者が情報の提供に消極的な事情さえ、国内の場合は強いと思います。著作権のかかわりが、どのように、工学技術の普及に貢献しているのか国内には全くといってよいほど見えてこない様相もひどいことは、欧米の工学書籍の内容を眺めてゆくと見えてきます。
例えば、ぜネバ機構の計算式、など国内の書籍では、ほとんど見られません。ＩＳＯとＡＷＳの溶接図示の比較文献も見たことがありません。そういった事情に鑑みて紹介記事を掲載しているのですが、やはり、著作権に関わってきます。サーバーにしても、維持費が高額で有償です。さらに、あれこれ、考えてゆくと、国内の機械設計環境の向上に向けるには、当方のブログはあまり貢献してしないという想いがあります。このあたりを考慮したのが本稿の趣旨です。ご了解お願いします。何かご意見などあればＥ－ｍａｉｌ頂ければと思います。
尚、独断ですが、有益性の高そうな書籍は、本ブログで、すでに紹介済です。

さし当たっては、当方のブログで必見の記事の紹介　当面行いたいと思います。

了

ソフト紹介：三次・四次方程式の解（2013/06/15） の訂正

表記の件、訂正いたしました。下記URL参照。
http://m-sudo.blogspot.jp/2013/06/blog-post_15.html

Casio 計算サイト　他　関係者の皆様に、謹んでお詫び申し上げます。
原因はExcelのセル幅が狭いために、真の値が丸められて表示されてしまったことが原因でした。内部演算は真の値で計算されています。Casioサイトでは。丸められた数字で計算していたもので誤差が生じました。この画面修正はデザインを損ねてしまうために、現状のままとします。入力値の検証は、上部の数式バーで確認されること記載しておきます。

２項係数の計算

http://m-sudo.blogspot.jp/2014/08/blog-post_10.html

http://math.stackexchange.com/questions/340124/binomial-coefficients-1-2-k

ちょっと難しい式ですが、設計には関係ない式です。(汗：メモ代わり）

但し、この２項係数使用の楕円周長は極めて扁平な楕円にあって楕円積分使用の数値よりは正確です。このあたり、後日紹介します。

構造：油圧シリンダのショック対策

上記データの引用元は下記。
https://www.nachi-fujikoshi.co.jp/tec/pdf/27D1.pdf
必読のファイルです。

関連Web
http://m-sudo.blogspot.jp/2012/07/blog-post_06.html

歯形係数を検証する。(Involute_Curve_3,1 を使用）：相手歯車の歯形係数、検証

前回の続きです。ここではバックラッシと歯形係数の関係性に焦点をあてています。互いに噛合う歯車の歯形係数は歯数の比に注意して吟味して決めることの重要性を指摘します。本ソフトが切り込んだ重要なポイントです。

バックラッシの中間の歯形は、CNC加工時の正規分布で有利な選択を可能に
します。バックラッシの最大時の選択は荷重条件の厳しい場合に、強度的にゆとりのある転位係数の選択を歯形係数という面から計算で検討することを可能にしています。（バックラッシとの関係において、歯形係数を考慮しない従来の設計手法では強度不足の可能性が計算過程から見えにくい状態であることがお判りと思います。）

歯形係数を検証する。(Involute_Curve_3,1 を使用）：データ入力～歯形係数の導出

記入データは旧ＪＩＳ3級、中心距離許容差はＪＧＭＡ規格Ｎ７，８級に合わせてみた。Ｎ７，８級は旧ＪＩＳにおいて、およそ3,4級相当のレベル。

上記手法を検討するに、旧JIS規格での歯車等級とバックラッシの対照表が新JGMAの規格から消えていることが惜しまれる。中心距離許容値との関係性も任意で決めることの困難さを見ます。今後の歯車間の設計はやはり、上図の３色の枠内の相互の関係性の中で決めてゆく手法に、無駄をなくすスマートさを見ることが可能と思います。新JGMAの規格では、この部分に代替可能な設計手法が、現在のところ見えてこないように思います。

歯車計算の仕様で中心距離は、設計者が最初に設定する項目と考えてよい。ここでは。設計中心距離は130ｍｍとあらかじめ設定されているものとした。結果的に113..011ｍｍとなったが、許容範囲内として認めた。転位係数を細かな桁数の数値にしてしまってはコストが高くつく。

バックラッシゼロの歯形係数と比較すると、0.1以上の差がついている。歯形係数は、バックラッシ最大時の計算を採用する考え方もあり、その場合は歯形係数の差はもっと大きくなります。

上記手順は歯形係数の実際的な使い方を示しています。

この転位係数を定めることに大変な時間を費やしますが、本ソフトの利用によって、この手間がかなり省力化されます。というより、この手法は本ソフトがなければ不可能だったと確信します。バックラッシと転位係数の関係に切り込んだソフトウエアと敢えて自賛します。

曲がり梁（Curved Beam)のデータ集

曲がり梁に関するデータを pdf データとして作成しました。
必要な方はダウンロードされてください。
http://m-sudo.sakura.ne.jp/soft_data/kikaikougaku(PDF)/Mgarihari%20No%20De-ta%20Syuu.pdf

下記ＵＲＬも参考にされてください。
http://m-sudo.blogspot.jp/2013/03/blog-post_24.html

動燃保護管折損事故対策_保護管の設計

表題の件、読み込み可能に設定しました。（一定期間公開予定）
内容に鑑みて、随時読込み不可にする予定。

http://m-sudo.sakura.ne.jp/soft_data/kikaikougaku(PDF)/Dounen_Jikotaisaku_Hogokan_SekkeiRei_Okazakikennkyuusyo.pdf

溶接記号表示の比較 ISO / AWS

英文だが、溶接記号の比較、検討に最適の文書。下記から直接ダウンロード可能のようです。当方のブログの画像よりは、こちらが間違いがない。当ブログの画像を設計データとしての利用は、背景を確認してからにして欲しい。（溶接に限らず）
海外の溶接関連の製図法の習得に座右におきたい一冊・

http://yusuf.mansuroglu.com/Welding_Symbols_on_Drawings.pdf#search='Welding_Symbols_on_Drawings.pdf'

機械製図で ISO と ANS I の差異が大きいのは溶接関連の図面表記です。一角法ベースの ISO と三角法ベースのAWS の差異はコツを知らなければ、習得は一筋縄ではゆかない。

歯形係数 ISO と AGMA

下図の変数記号の詳細については、最下段のURLからｐｄｆ文書（英文）のダウンロードをされたうえで、確認してください。下図は概要のみ表示しています。

図は下記URLより
http://www.researchgate.net/publication/245366730_Comparative_Analysis_of_Tooth-Root_Strength_Using_ISO_and_AGMA_Standards_in_Spur_and_Helical_Gears_With_FEM-based_Verification

当方はこの論文の意図するところがよく見えないので、情けないのだが、興味をもたれた方には、参考論文を探し出して、この論文の意図するところを読まれて欲しい。
私でも、判ることは、歯形係数を求める式の構造が,ISO とAGMAでは全く異なることだが、強度計算の式もまた異なる表記になっている。（上記WEB参照）
AGMAの歯形係数の計算式を上記WEBによって初めて知った。（現在でも同様かは不明。）

上記文献を当方で編集（全文）、ダウンロードを可能にしてみた。歯形係数の両規格の計算式、歯元応力の計算式(2006年次)が記載されています。

http://m-sudo.sakura.ne.jp/soft_data/kikaikougaku(PDF)/Comparative%20Analysis%20of%20...pdf

動摩擦係数

出典は下記。
http://www.designnotes.com/companion/manual-2.html
追記)2015.07.19 上図が違っていたので削除のうえ、新規に図を挿入しました。

出典は下記。
http://www.riruraru.com/cfv21/phys/friction.htm

下記ファイル訂正のうえ、ダウンロード可能にしました。(2015.07.20)
http://m-sudo.sakura.ne.jp/soft_data/kikaisekkei_data/Masatukeisuu_de-ta_syuu.pdf
(摩擦係数データ集：静摩擦係数、動摩擦係数、転がり摩擦係数）

Involute_Curve_3.1 の フル画面イメージ（Ｔｅｓｔ）

エクセルのスプレッドシート一杯の画面をうまく投稿できるかテスト中です。画像の拡大が効くかどうか。エクセル以外の画面でできないか検討中です。

下記操作でダウンロードすることが現在のところ唯一の方法だが・・・
http://m-sudo.sakura.ne.jp/soft_data/gazou_data/Involute_Curve_3.1%20Full%20image_1.png
http://m-sudo.sakura.ne.jp/soft_data/gazou_data/Involute_Curve_3.1%20Full%20image_2.png
今のところ、Google Chrome で上記で取り込み、Google_Chome で拡大操作でＯＫだが・・・
Internet Explorer でも拡大操作でＯＫ・・・　もっと良い方法がないか？？？
今回のUPはちょっと特別な手法を利用。Internet Explorerではダメかもしれない。

Involute_Curve_3.1 試行版のダウンロードが可能です。

下記よりダウンロード（取得）可能です。
http://m-sudo.sakura.ne.jp/soft_data/Excel2003_VBA_soft/Involute_Curve_3.1_Test_Version.zip

試行版ソフト本体
簡易操作説明書
もうひとつファイルがあるのですが、こちらは無視してください。(データが旧ソフトに拠るため）

制限事項
モジュール　ｍ＝５　
二つの歯車の歯数の和が35以下
歯数は１３以上（本歯車、相手歯車　共通）
試用版は無償です。制限事項以外は全機能が使用可能です。

追記)2015.07.17
歯数　13～22までならば、正確な歯形係数を算出します。(相手歯車も同条件）

中心距離から転位係数を求める_3

表記の件、Involute_Curve_3.1 訂正版の出力値比較表 を　作成してみました。

中心距離から転位係数を求める_2

表記の件について、結論を先に記載しておきます。

１）頂げき一定方式を基本に。歯たけ一定方式は性能（騒音、噛合い率など）を極めるに適していますが、頂げきが不足することによる、潤滑油の劣化、歯面損傷、発熱など装置寿命に関する否定的な影響が比較的に大きい。

２）転位係数は歯数の多い方のデータを大きくする（+-の符号をも)考慮。歯数差が大きい場合は、歯形係数の確認が欠かせない。歯形係数は双方同じ数値が理想的。注意することは、切下げにかからないこと。切下げが生ずると歯形係数は一気に増加してしまいます。

３）中心距離の許容値とまたぎ歯厚許容値の関係はトレードオフにある。歯車の精度が高ければ中心距離許容値が緩やかだが、中心距離許容値を厳しくすると、歯車の精度確保に余裕が生じてくる（バックラッシなど）。従って、歯車箱（Gear Box)のボーリング穴間の許容値はコストが許す限り小さな範囲に収めるべきです。その結果歯車の円弧歯厚の許容値は大きく取れます。

ISO規格は歯形係数の算出を推奨しており、グラフの活用は勧めていません。
国内には当方作成のソフト以外には的確な算出ソフトは（１００万円前後のよほど高価なソフトでない限り）入手は困難です。昔、芝浦工業大学関連でExcel
VBAを利用したソフトがあったかと思いますが、バックラッシのための円弧歯厚減少加工歯形には対応していなかったと思います。

本ブログページのＰＤＦ化について

標記の件、可能ならAdobe社の　Adobe Acrobat Professionalの最新版があればよいのですが、高価なために、Micro Soft社のWindowsを利用しての、印刷機能からのPDFデータ化を薦めます。Google Chrome の使用も場合によってはよいかも知れません。PDF化する際は、本ブログの場合、タイトルごとにPDF化する方法を薦めます。

中心距離から転位係数を求める_1

Involute_Curve_3.1 を使用して転位係数を求める方法。

とりあえず、転位係数を求めてみます。本来、ここで求めた転位係数は、かみ合い率、頂げき、さらに、歯形係数の検討を行って、歯車の仕様計算法としての、転位時：頂げき一定モード、転位時：歯たけ一定モードの選択までさかのぼって検討するのが望ましいのですが、常識的には、転位時：頂げき一定モードと決めて設計計算を行うのが間違いが少ないと思います。転位時：歯たけ一定モードは、装置寿命を損ねる危険性が高いので薦められません。但し、転位係数を求める計算自体はどちらのモードでも同じ結果を得ます。

次回は求めた転位係数の検討手法について説明予定です。

数値積分の活用（ガウス-レジャンドル法）

楕円積分、２次以上の関数で示される曲線で囲まれた部分の面積など数値積分を強いられることがままある。高校数学ではシンプソンの積分などを習うが、誤差の収束が遅く、正確さがいまひとつ足りない不安を強いられた経験をされた方は多いと思う。この十数年の間にＭｉｃｒｏｓｆｔ社のＥｘｃｅｌが普及し、高精度の数値計算が可能になった。電卓程度で計算せざるを得なかった時代ではシンプソンの数値計算は必須ともいえたが、現代では、使う気になれない。ガウス・レジャンドル法というプログラム向きで高精度の手法の使用が、現代の数値積分と思います。
この背景にはＥｘｃｅｌ－ＶＢＡの計算精度の向上があり、通常の加減乗除計算で有効数字が制限一杯誤差ゼロに収めることが容易になったことがあげられます。16桁以上の高精度演算にはＣ++が必要と思うが、とても一般向きには使い難い欠点があります。

当方の作成したソフトの中に楕円積分計算ソフト(有償:2000円)がありますが、この有償版はプログラムコードを公開しています。このプログラム手法を応用することで、ガウス-レジャンドル法の数値積分の世界が広がります。このソフトのご活用をぜひ、ご検討お願いします。

詳しくは過去ブログをどうぞ

ガウス_レジャンドルのデータ計算ソフト

画像は数値積分_ガウス_レジャンドル法の使用に必要なデータを求めるソフトウエア。有限会社ゴッドフット企画のＷｅｂ（http://homepage1.nifty.com/gfk/）から基幹部分を導入し、Ｅｘｃｅｌで使用し易いようにデータ群を抽出する当方作成のソフトウエアです。プログラムコードは公開してあります。

本ソフトは下記ＵＲＬから取得可能です。
http://m-sudo.sakura.ne.jp/soft_data/Excel2003_VBA_soft/Takousiki_Kai_keisan.zip
または
http://m-sudo.sakura.ne.jp/soft_data/Excel2003_VBA_soft/

本ソフトの最大項数は表計算活用可能なセル数だけ可能ですが、楕円積分の精度を考えると1300程度が実際的な項数と思います。これ以上の項数になるとＥｘｃｅｌ自体の計算誤差の蓄積が目立ってしまいます。かなり扁平な楕円周長の計算でも1264項で有効数字14桁にわたって正確な数値をたたきだします。

３次方程式ソフトウエアに見るExcel(VBA)の計算精度

上図、計算結果を比較されたい。当方作成のソフトで有効数字15桁が完全に左側のWebの解析結果と一致しています。当方は、精度を確保するために特別な手法を凝らした訳ではないのですが、Excel(VBA)の計算精度の高さが際立ちます。
左側のWebは下記。
www.akiti.ca/Quad3Deg.html

重要：本ブログの検索エンジンの閲覧を拒否設定にしました。（一定期間）

Googleｎ画像検索がちょっとひどいので、当分の間、検索エンジンの閲覧を
拒否に設定しました。将来、元に戻すかもしれませんが。

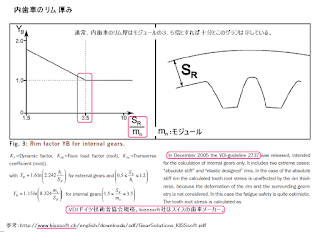
再掲載：歯車のリムの厚み

下記URLも参照。（内容は重複します。）
http://m-sudo.blogspot.jp/2014/02/blog-post_6461.html

本データの原本（PDF）は下記より取得
www.kisssoft.ch/english/downloads/pdf/GearSolutions_KISSsoft.pdf

当方のサーバーよりからも取得可能
http://m-sudo.sakura.ne.jp/soft_data/kikaikougaku(PDF)/GearSolutions_KISSsoft.pdf

本データはISO規格の影響下ですが、AGMA（USA：全米歯車協会）においてもこのデータが採用されているようです。（ISOの方が後で採用）

尚、歯幅が広い平歯車の場合は下記を参照。

追記(2014.03.07記)

  上図のＳRを求めるにあたって、歯幅をＢとするとき　SR=2.2*m+B*0.05 を採用する考え方もある。

偽メール！

yahooに通知しましょう。