m-sudo's Room: 曲線（楕円）の曲率半径・接線の傾き

2010/10/12

画像は下記URLより

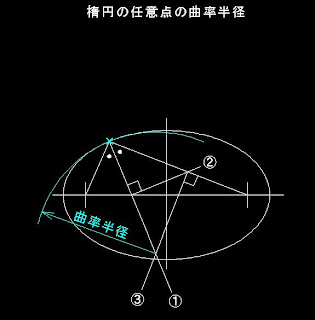
楕円歯車の歯形作成に必要な楕円周上の点の曲率半径を求める式。

（上図の説明では楕円に限らず微分可能な関数で表示可能な曲線に一般化しているとみてよい。）

画像は下記URLより

画像は下記URLより

画像は下記URLより

画像は下記URLより

AutoCAD_LTを利用して作図したCAD図小数点以下５桁あたりで誤差が出ている可能性はあるが、検証用として利用できる。

楕円周上45°の位置での曲率半径を計算で求めてみる。

曲率半径(r)=((a^2*(sinθ)^2+b^2*(cosθ)^2)^(3/2))/(a*b)

=((100^2*(sin63.26291)^2+50^2*(cos63.26291)^2)^(3/2))/(100*50)

=156.2331078（上図では156.732255となっているがCADの誤差だろう。）

ここでθは楕円上の点をパラメータ表示したとき

x=a*cosθ

y=b*sinθ

を満足する角度(0 =< θ =< 2π）。

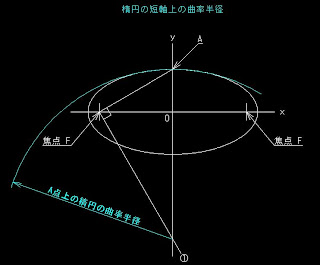
楕円の曲率半径を求める式は下図

画像の引用元は下記ＵＲＬ

追記）当方で楕円緒量を求めるソフトを作成、無償公開しています。

下記URLからどうぞ

本ソフトはVectorからも公開予定です。

m-sudo's Room