平板のたわみ計算_全周固定

画像は下記ＵＲＬより。
http://www.efunda.com/formulae/solid_mechanics/plates/calculators/SSSS_PUniform.cfm
古典的と評価された記事を見かけたような気がするが、有益な計算式。ここのｅｆｕｎｄａの計算Ｗｅｂは利用価値があります。周辺固定と周辺支持の組合せの計算式など機会を見ては紹介予定。
上図中下部の計算は２＊２次(n,m=1,3）ですが設計的にはこれで十分でしょう。
下記ＵＲＬも参照。
http://m-sudo.blogspot.jp/2010/10/w.html
http://m-sudo.blogspot.jp/2013/09/blog-post_21.html

レイノルズ数＿層流と乱流

必要があってレイノルズ数の確認を行ったが、久しぶりに層流と乱流の境目の数値を調べた。ネットで調べるといろいろな数値が飛び交っている。当方の独断でまとめてみたのでご参考に。

関係分野：　油圧装置設計
レイノルズ数と層流、乱流の関係：
　　　　　　　　レイノルズ数：Ｒｅ
　　　　　　　　層流：　1500以下
　　　　　　　　乱流：　3200以上
　　　　　　　　遷移領域：1500～3200

参考に油圧機器メーカーの油研工業（株）のカタログでは2300を層流と乱流の境目としている。
http://www.yuken.co.jp/japanese/product/pro_sogo09/pdf/z1/z1-1-2009.pdf

もう一つ参考に（株）神鋼ソルーションのＷｅｂでは下図。
http://www.kobelco-eco.co.jp/product/process/mixing/mixing_002.htmlより

上図の記述の数値も根拠にされてよい十分な数値と思います。

技術者Ｗｅｂ学習システム

筆者の現在の勤務先で紹介されたＷｅｂ学習システムのＵＲＬ。専門外の業務に係ったときにとても参考になった。

ちなみに筆者が長年係ってきた関係の学習内容。この大筋は専門であればそらんじて瞬時に想起可能なレベルである。このＷｅｂのＵＲＬは下記。

http://weblearningplaza.jst.go.jp/cgi-bin/user/lesson_start.pl?course_code=298&lesson_code=2740&now_course=298

ガウスレジェンドル法の積分点計算（英語版）

画像は当方のＵＲＬ下記より
http://vanlover.blogspot.jp/
積分のコンピュータ利用の数値計算法としては極めて高精度の算出が可能。
英語版も用意しているが、こちらの累積アクセス数も高い。

Ｈ２Ａ商業衛星として打上げ成功

画像は産経新聞社のＵＲＬより。
Ｈ２Ａロケットの設備開発設計に少しばかり係った筆者にとってよきニュースだった。宇宙関連では他のメーカーでも衛星筐体（シェル）の生産設計に係った経験もあり、宇宙産業の進展は嬉しいものがある。

４次方程式、３次方程式の解法

画像は下記ＵＲＬより引用。
http://galois.motion.ne.jp/stories/G_Math_07.html
上記図は２次方程式、３次方程式、４次方程式の複素数表現でのそれぞれの解の配置の相互関係を示しています。小生が作成したソフトの解の検証に上記の複素数の等分された角度配置の確認を行っていました。小生はフェラーリの解法を忠実に追って３次方程式、４次方程式の解を求めたのですが、上記ＵＲＬには３次方程式、４次方程式の解を求める数式の記述があります。時間がないので確認をとったわけではないのですが、興味のある向きは覗かれるのもよろしいかと・・・。
下図は４次方程式の数式解の一端。これも上記ＵＲＬより引用。
尚，図中のリゾルベントという言葉には小生は全く知識を持っていません。
キーワード：３次、４次方程式　代数解、複素数

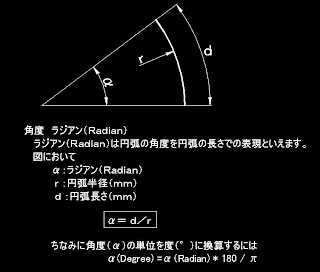
角度単位 ラジアン（Ｒａｄｉａｎ）

Ｅｘｃｅｌ　を利用するときの角度単位はラジアン（Ｒａｄｉａｎ）です。普段は角度単位には度（Ｄｅｇｒｅｅ）を利用しているので若干の違和感を抱きます。図のように意味合いを明示すると違和感が軽減されると思われますが、いかがでしょうか。
追記）上図中
　　　ラジアン(Radian)円弧の角度を円弧長さでの表現といえます。
　　　＝＝＞ラジアン(Radian)円弧の角度を、円弧長さと半径の比で表現したものといえます。
　　　読み替えてください。